הנושא של מאמר זה הוא חישוב של חופה פוליקרבונט במו ידיך. עלינו ללמוד כיצד לחשב את הפרמטרים העיקריים של המבנה הקשורים לחוזק ולמידות שלו. אז בוא נלך.

מה אנחנו מחשבים
עלינו ללמוד כיצד לחשב:
- עובי הפוליקרבונט וגובה הארגז בהתאם לעומס השלג הצפוי למ"ר.
- מידות כיסוי קשת (מה שמבחינת גיאומטריה מסתכם בחישוב אורך הקשת).
להבהיר: אנו בוחנים דרכים לחישוב הקשת עבור רדיוס וזווית ידועים של הגזרה, כמו גם למקרה שבו אנו יודעים רק את המרחקים בין הנקודות הקיצוניות של פני הקשת.
- חתך צינור מינימלי עם עומס כיפוף ידוע.
לפי הסדר הזה, נמשיך הלאה.
עובי חרטה וציפוי
נתחיל בחישוב עומס השלג.
לפני שנבין כיצד לחשב חופה מפוליקרבונט, ננסח כמה הנחות שעליהן מתבסס החישוב.
- הנתונים המפורטים רלוונטיים לחומר באיכות גבוהה ללא סימני הרס בקרינה אולטרה סגולה. פוליקרבונט ללא מסנן UV הופך שביר לאחר 2-3 שנות פעילות באור.

- אנו מזניחים בכוונה את יציבות העיוות המוגבלת של הארגז, בהתחשב בכך שהיא חזקה לחלוטין.
ועכשיו - טבלה שתעזור לכם לבחור את העובי האופטימלי של הפוליקרבונט ואת גובה הארגז.
| עומס, ק"ג/מ"ר | מידות תא ארגז בעובי פוליקרבונט, מ"מ | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200x900 | 1320x920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880x660 | 1000x750 | 1050x750 | 1150x900 |
| 760x760 | 830x830 | 830x830 | 970x970 | |
| 700x860 | 750x900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950x700 | 1100x850 |
| 690x690 | 760x760 | 780x780 | 880x880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
קֶשֶׁת
חישוב לפי רדיוס ומגזר
כיצד לחשב את הקשת לחופה אם אנו יודעים את רדיוס הכיפוף וגזרת הקשת?

הנוסחה תיראה כמו P=pi*r*n/180, כאשר:
- P הוא אורך הקשת (במקרה שלנו, אורך יריעת פוליקרבונט או צינור פרופיל, שיהפוך לאלמנט של המסגרת).
- pi הוא המספר "pi" (בחישובים שאינם דורשים דיוק גבוה במיוחד, בדרך כלל שווה ל-3.14).
- r הוא רדיוס הקשת.
- n היא זווית הקשת במעלות.
בואו, כדוגמה, לחשב במו ידינו את אורך קשת החופה ברדיוס של 2 מטר וגזרה של 35 מעלות.
P \u003d 3.14 * 2 * 35 / 180 \u003d 1.22 מטר.
בתהליך העבודה, לעתים קרובות מתעורר המצב ההפוך: יש צורך להתאים את הרדיוס והגזרה של הקשת לאורך קבוע של הקשת. הסיבות ברורות: מחיר הפוליקרבונט גבוה מספיק כדי למזער את כמות הפסולת.
ברור שבמקרה זה מכפלת הסקטור והרדיוס יהיו שווה ל-P/pi*180.
בואו ננסה להתאים את הקשת מתחת ליריעה סטנדרטית באורך 6 מטרים. 6/3.14*180=343.9 (עם עיגול). יתר על כן - מבחר פשוט של ערכים עם מחשבון ביד: לדוגמה, עבור מגזר קשת של 180 מעלות, אתה יכול לקחת את הרדיוס השווה ל-343.9 / 180 \u003d 1.91 מטר; עם רדיוס של 2 מטרים, המגזר יהיה שווה ל-343.9 / 2 \u003d 171.95 מעלות.
חישוב לפי אקורדים
איך נראה חישוב העיצוב של חופה מפוליקרבונט עם קשת אם יש לנו רק מידע על המרחק בין קצוות הקשת לגובהה?
במקרה זה, הנוסחה שנקראת Huygens מיושמת. כדי להשתמש בו, בואו נחלק מנטלית את האקורד המחבר את קצוות הקשת לשניים, ולאחר מכן נצייר מאונך לאקורד באמצע.
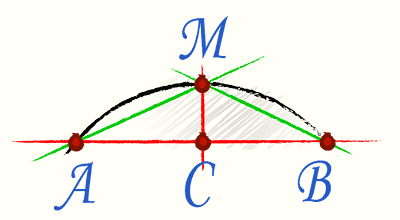
לנוסחה עצמה יש את הצורה Р=2l+1/3*(2l-L), כאשר l הוא אקורד AM ו-L הוא אקורד AB.
חשוב: החישוב נותן תוצאה משוערת. השגיאה המקסימלית היא 0.5%; ככל שהמגזר הזוויתי של הקשת קטן יותר, השגיאה קטנה יותר.
בואו לחשב את אורך הקשת עבור המקרה כאשר AB \u003d 2 מ 'ו AM - 1.2 מ'.
P=2*1.2+1/3*(2*1.2-2)=2.4+1/3*0.4=2.533 מטר.
חישוב הקטע עם עומס כיפוף ידוע
די מצב חיים: חלק מהחופה הוא מצחייה באורך ידוע. אנו יכולים להעריך באופן גס את שיא עומס השלג עליו. איך לבחור צינור פרופיל של קטע כזה לקורות כך שהוא לא יתכופף תחת עומס?

הערה! אנחנו בכוונה לא נוגעים איך לחשב את העומס על החופה. הערכת עומס שלג ורוח היא נושא עצמאי לחלוטין למאמר נפרד.
כדי לחשב, אנחנו צריכים שתי נוסחאות:
- M = FL, כאשר M הוא מומנט הכיפוף, F הוא הכוח המופעל על קצה הידית בקילוגרמים (במקרה שלנו, משקל השלג על המצחייה), ו-L הוא אורך הידית (האורך של הקורה הנושאת את העומס מהשלג, מחברי קצה לנקודה) בסנטימטרים.
- M/W=R, כאשר W הוא רגע ההתנגדות ו-R הוא חוזק החומר.
ואיך ערימת הערכים הלא ידועים הזו תעזור לנו?
כשלעצמו, כלום. חסרים כמה נתוני התייחסות לחישוב.
| כיתה פלדה | חוזק (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
התייחסות: פלדות St3, St4 ו-St5 משמשות בדרך כלל לצינורות מקצועיים.
כעת, בהתבסס על הנתונים שבידינו, אנו יכולים לחשב את מומנט ההתנגדות לכיפוף של צינור הפרופיל. בוא נעשה את זה.
נניח ש-400 קילוגרמים של שלג מצטברים על חופה של שני מטרים עם שלוש קורות נושאות עשויות פלדת St3.כדי לפשט את החישובים, נסכים שהעומס כולו נופל על קצה המצחייה. ברור שהעומס על כל קורה יהיה 400/3=133.3 ק"ג; עם מנוף של שני מטרים, רגע הכיפוף יהיה שווה ל 133.3 * 200 \u003d 26660 kgf * ס"מ.
כעת אנו מחשבים את מומנט ההתנגדות W. מתוך המשוואה 26660 kgf * cm / W = 2100 kgf / cm2 (חוזק פלדה) יוצא שרגע ההתנגדות צריך להיות לפחות 26660 kgf * cm / 2100 kgf / cm2 = 12.7 cm3.
כיצד יוביל אותנו ערכו של רגע ההתנגדות למידות הצינור? דרך טבלאות המבחר הכלולים ב- GOST 8639-82 ו- GOST 8645-68 המסדירים את הממדים של צינורות מרובעים ומעוצבים. עבור כל גודל, הם מציינים את רגע ההתנגדות המתאים, ולחתך מלבני - לאורך כל אחד מהצירים.
לאחר בדיקת הטבלאות, אנו מגלים כי הגודל המינימלי של צינור מרובע עם המאפיינים הנדרשים הוא 50x50x7.0 מ"מ; מלבני (עם כיוון אנכי של הצד הגדול יותר) - 70x30x5.0 מ"מ.

סיכום
אנו מקווים שלא עבדנו יתר על המידה על הקורא עם שפע של דמויות ונוסחאות יבשות. כמו תמיד, מידע נוסף על השיטות לחישוב ועיצוב חופות פוליקרבונט ניתן למצוא בסרטון במאמר זה. בהצלחה!
המאמר עזר לך?